
There are no numbers that are simultaneously larger than 2 and less than -2

In a quadratic inequality like you're working with, there are generally an infinite number of solutions.įor this inequality (it's not an equation) to be satisfied it must be true that: In a quadratic equation you can have at most two solutions. There's a big difference between equations and inequalities. Sorry for the remedial questions! Thanks for the explanations!
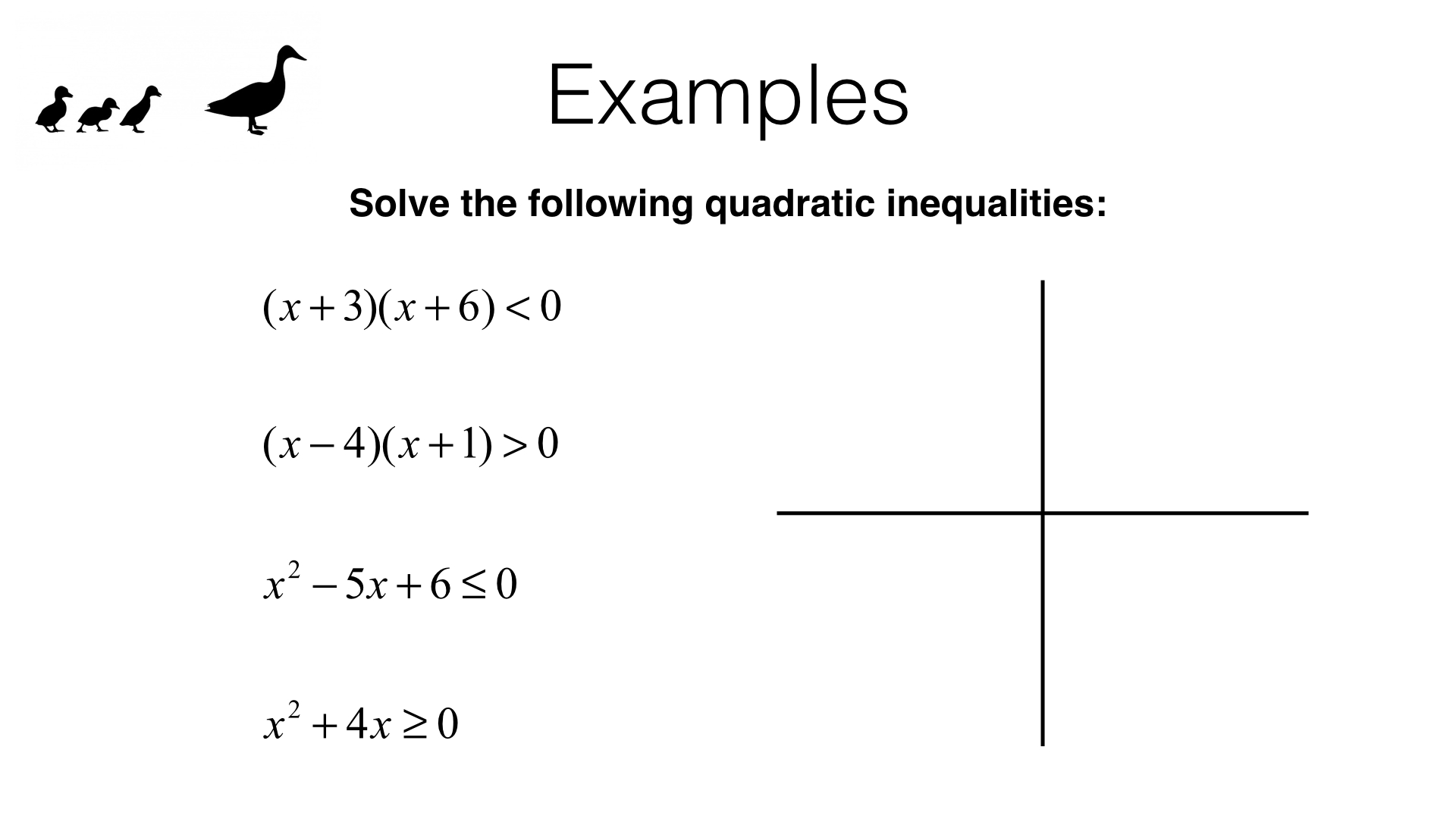
I understand that the two numbers work, but how do I know to flip the sign (to less than in this case) and look for that second set of possibilities? I also don't understand how I know when I'm looking for an "Or" and when I'm looking for an "And" combination? X 0 we've not only got those first two possibilities x > -3 x > 3]īut two new possibilities appear when the sign gets switched [x 3 or x<-3. While the answers are correctly written, I mistyped the signs in the work. If the work below is the same as what's in the book, and the problem is as above, the book's answer is wrong. They can't have mixed signs as shown below. If two factors multiply to make a positive product, then either both factors are positive, or both are negative. How do we know to also add (or look for) x 0 Sorry, using the template doesn't make much sense here, but I'm using it b/c it says to.Īnd then cross out x > - 3 b/c it doesn't work, leaving only x > 3? Please help me understand why the book switches the sign without explaining why! I understand the particular answers but can't derive a rule of thumb. I'll go through them sequentially I'm trying to understand the concept, not the particular answer. I don't see how or why the sign reversal arises and the second set of options comes up.
#Solving quadratic inequalities how to#
I'm confused b/c I understand how to solve them with an = sign, but as inequalities the book shows extra steps where signs get reversed and a total of ~ 4 possible answers come up instead of 2. Then we can solve the inequality.Here are two, unconnected example problems, having to do with quadratic inequalities. We can factorize the quadratic expression with the help of the above quadratic formula. Here we obtain α = -1 and β = 1, and the range of x is x ∈ \). The expression x 2 - 1 > 0 can be factorized as (x - 1)(x + 1) > 0. If the quadratic inequality is x 2 - 1 0 (where it shows the quadratic inequality is greater than or equal to zero). Hence, we obtain the range of x as x ∈ (-∞, -1) U (1, + ∞)

This gives the values of α = -1 and β = 1. Here the expression x 2 - 1 > 0 can be factorized as (x - 1)(x + 1) > 0. We can write the quadratic expression in the form of (x - α)(x - β) and α 0, then x can take values between - ∞ to α and β to +∞. Now consider a quadratic expression ax 2 + bx + c. Solving a quadratic inequation means finding the range of values of x. It can have infinite values of x which satisfy the condition ax 2 + bx + c 0. But a quadratic inequality can have more than 2 values. A quadratic second degree equation ax 2 + bx + c = 0 can have maximum 2 values of x.
Solving a quadratic inequality means to find the values of x which satisfy the given condition of the question. Thus, the quadratic inequality for the above scenario is as follows. Now, we know that the area cannot exceed 1500 ft 2. Hence, the area of the house is (2 + 2x)x = 2x 2 + 2x, where x is the breadth of the rectangular house. You know that the area of a rectangle is length times its breadth. If you don't want the floor area of the house to be more than 1500 ft 2, what length and breadth can you consider? Now, consider the scenario where you want to build a rectangular house with a length equal to two units more than twice its breadth. The standard form of quadratic inequality can be represented as: The quadratic inequality is a second-degree expression in x and has a greater than (>) or lesser than ( 0 What Do You Mean By Quadratic Inequalities?


 0 kommentar(er)
0 kommentar(er)
